Can I Change From J2 To J1

Similar Merge Sort, QuickSort is a Divide and Conquer algorithm. It picks an chemical element as pin and partitions the given array around the picked pivot. There are many different versions of quickSort that choice pivot in different ways.

1. Always pick first chemical element as pin.
2. E'er option last chemical element as pin (implemented below)
3. Option a random element as pin.
4. Pick median as pivot.

The fundamental process in quickSort is partition(). Target of partitions is, given an array and an element x of assortment as pin, put x at its correct position in sorted array and put all smaller elements (smaller than x) before x, and put all greater elements (greater than x) after x. All this should be done in linear fourth dimension.

Pseudo Code for recursive QuickSort office :

/* low  --> Starting index,  high  --> Ending alphabetize */ quickSort(arr[], low, high) {     if (depression < loftier)     {         /* pi is partitioning index, arr[pi] is at present            at right place */         pi = partition(arr, low, high);          quickSort(arr, low, pi - ane);  // Before pi         quickSort(arr, pi + 1, loftier); // After pi     } }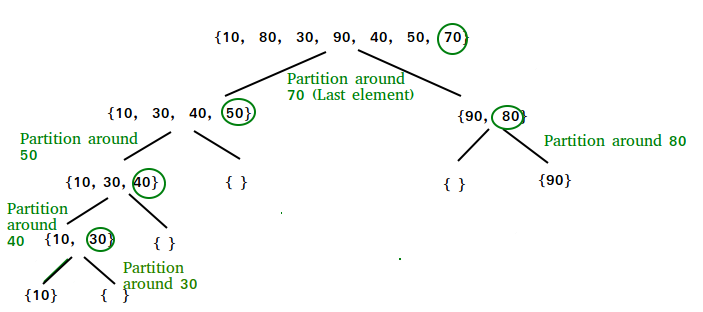

Segmentation Algorithm
There can exist many ways to practice sectionalisation, following pseudo code adopts the method given in CLRS book. The logic is elementary, we beginning from the leftmost chemical element and go on rail of index of smaller (or equal to) elements as i. While traversing, if we notice a smaller chemical element, we swap current element with arr[i]. Otherwise we ignore electric current element.

/* low  --> Starting index,  high  --> Ending index */ quickSort(arr[], depression, loftier) {     if (low < high)     {         /* pi is partitioning alphabetize, arr[pi] is now            at correct place */         pi = sectionalization(arr, low, high);          quickSort(arr, low, pi - 1);  // Before pi         quickSort(arr, pi + 1, high); // After pi     } }

Pseudo lawmaking for division()

/* This part takes last chemical element equally pivot, places    the pivot chemical element at its right position in sorted     array, and places all smaller (smaller than pivot)    to left of pivot and all greater elements to right    of pin */ segmentation (arr[], low, high) {     // pivot (Element to be placed at right position)     pivot = arr[loftier];         i = (low - i)  // Index of smaller element and indicates the                     // right position of pivot plant so far      for (j = low; j <= loftier- ane; j++)     {         // If current element is smaller than the pivot         if (arr[j] < pivot)         {             i++;    // increase alphabetize of smaller element             swap arr[i] and arr[j]         }     }     swap arr[i + ane] and arr[high])     render (i + 1) }

Illustration of partition() :

arr[] = {ten, eighty, 30, 90, 40, fifty, 70} Indexes:  0   1   2   3   4   5   6   depression = 0, loftier =  6, pin = arr[h] = 70 Initialize alphabetize of smaller element,          i = -i          Traverse elements from j = low to high-1          j = 0          : Since arr[j] <= pin, do i++ and bandy(arr[i], arr[j])          i = 0                    arr[] = {ten, fourscore, thirty, xc, twoscore, 50, 70} // No change as i and j                                       // are same          j = one          : Since arr[j] > pin, do nothing // No alter in i and arr[]          j = 2          : Since arr[j] <= pivot, practise i++ and bandy(arr[i], arr[j])          i = ane          arr[] = {ten, 30, lxxx, 90, 40, fifty, 70} // Nosotros bandy 80 and 30          j = 3          : Since arr[j] > pivot, do nothing // No change in i and arr[]          j = 4          : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])          i = two          arr[] = {x, 30, 40, 90, eighty, 50, lxx} // 80 and 40 Swapped          j = 5          : Since arr[j] <= pivot, do i++ and bandy arr[i] with arr[j]          i = 3                    arr[] = {10, 30, twoscore, l, 80, ninety, seventy} // 90 and 50 Swapped   We come out of loop because j is now equal to high-1.          Finally we place pivot at correct position by swapping          arr[i+1] and arr[loftier] (or pivot)          arr[] = {x, 30, 40, 50, 70, 90, fourscore} // lxxx and seventy Swapped   At present 70 is at its correct place. All elements smaller than 70 are earlier it and all elements greater than 70 are later on it.

Recommended: Please solve it on " Do " first, before moving on to the solution.

Implementation:
Post-obit are the implementations of QuickSort:

C++xiv

#include <bits/stdc++.h>

using namespace std;

void swap( int * a, int * b)

{

int t = *a;

*a = *b;

*b = t;

}

int segmentation ( int arr[], int low, int loftier)

{

int pivot = arr[high];

int i = (low - i);

for ( int j = low; j <= high - 1; j++)

{

if (arr[j] < pivot)

{

i++;

bandy(&arr[i], &arr[j]);

}

}

swap(&arr[i + 1], &arr[high]);

return (i + 1);

}

void quickSort( int arr[], int low, int high)

{

if (low < high)

{

int pi = sectionalisation(arr, low, high);

quickSort(arr, low, pi - i);

quickSort(arr, pi + 1, high);

}

}

void printArray( int arr[], int size)

{

int i;

for (i = 0; i < size; i++)

cout << arr[i] << " " ;

cout << endl;

}

int main()

{

int arr[] = {x, vii, viii, 9, 1, five};

int due north = sizeof (arr) / sizeof (arr[0]);

quickSort(arr, 0, north - ane);

cout << "Sorted array: \n" ;

printArray(arr, n);

return 0;

}

Coffee

import java.io.*;

course GFG{

static void swap( int [] arr, int i, int j)

{

int temp = arr[i];

arr[i] = arr[j];

arr[j] = temp;

}

static int partition( int [] arr, int low, int high)

{

int pin = arr[high];

int i = (low - 1 );

for ( int j = depression; j <= high - ane ; j++)

{

if (arr[j] < pivot)

{

i++;

swap(arr, i, j);

}

}

swap(arr, i + ane , high);

return (i + i );

}

static void quickSort( int [] arr, int depression, int high)

{

if (depression < loftier)

{

int pi = segmentation(arr, low, high);

quickSort(arr, low, pi - 1 );

quickSort(arr, pi + ane , high);

}

}

static void printArray( int [] arr, int size)

{

for ( int i = 0 ; i < size; i++)

Arrangement.out.print(arr[i] + " " );

System.out.println();

}

public static void principal(String[] args)

{

int [] arr = { 10 , seven , viii , nine , 1 , 5 };

int n = arr.length;

quickSort(arr, 0 , north - 1 );

Organization.out.println( "Sorted assortment: " );

printArray(arr, n);

}

}

Python3

def partition(commencement, stop, assortment):

pivot_index = start

pivot = assortment[pivot_index]

while start < end:

while outset < len (array) and array[commencement] < = pivot:

beginning + = 1

while array[end] > pin:

end - = 1

if (commencement < finish):

array[beginning], array[end] = array[terminate], array[start]

array[terminate], array[pivot_index] = assortment[pivot_index], array[end]

render end

def quick_sort(get-go, end, assortment):

if (offset < end):

p = partitioning(offset, finish, array)

quick_sort(offset, p - ane , array)

quick_sort(p + 1 , end, array)

array = [ 10 , vii , 8 , ix , one , five ]

quick_sort( 0 , len (assortment) - 1 , array)

print (f 'Sorted array: {array}' )

Javascript

<script>

role swap(arr, i, j) {

let temp = arr[i];

arr[i] = arr[j];

arr[j] = temp;

}

part partition(arr, low, high) {

let pivot = arr[high];

let i = (low - i);

for (let j = low; j <= high - 1; j++) {

if (arr[j] < pivot) {

i++;

bandy(arr, i, j);

}

}

swap(arr, i + 1, high);

return (i + 1);

}

role quickSort(arr, low, loftier) {

if (low < high) {

let pi = partition(arr, low, high);

quickSort(arr, low, pi - ane);

quickSort(arr, pi + i, high);

}

}

part printArray(arr, size) {

for (let i = 0; i < size; i++)

certificate.write(arr[i] + " " );

certificate.write( "<br>" );

}

let arr = [x, 7, 8, ix, 1, 5];

let northward = arr.length;

quickSort(arr, 0, n - i);

certificate.write( "Sorted assortment: <br>" );

printArray(arr, n);

</script>

Output

Sorted array:  1 five 7 8 9 10          

Assay of QuickSort
Time taken by QuickSort, in general, can be written every bit following.

          T(due north) = T(k) + T(north-k-one) +          (n)

The first two terms are for 2 recursive calls, the terminal term is for the division process. thou is the number of elements which are smaller than pivot.
The time taken by QuickSort depends upon the input assortment and sectionalization strategy. Following are iii cases.

Worst Instance: The worst instance occurs when the partition process e'er picks greatest or smallest element as pivot. If we consider in a higher place segmentation strategy where terminal chemical element is always picked as pivot, the worst case would occur when the array is already sorted in increasing or decreasing order. Post-obit is recurrence for worst instance.

          T(n) = T(0) + T(north-1) +          (n)  which is equivalent to    T(due north) = T(n-i) +          (due north)

The solution of higher up recurrence is(north²).

Best Case: The best case occurs when the partition process ever picks the middle element every bit pivot. Following is recurrence for best case.

          T(n) = 2T(north/2) +          (n)

The solution of above recurrence is(nLogn). It tin can be solved using example 2 of Master Theorem.

Boilerplate Case:
To practice boilerplate case analysis, we need to consider all possible permutation of array and calculate time taken by every permutation which doesn't look easy.
We tin can get an idea of average case past considering the case when partition puts O(n/9) elements in i set and O(9n/10) elements in other set. Following is recurrence for this case.

          T(north) = T(n/ix) + T(9n/10) +          (n)

Solution of in a higher place recurrence is also O(nLogn)
Although the worst case time complication of QuickSort is O(northward²) which is more than many other sorting algorithms like Merge Sort and Heap Sort, QuickSort is faster in practice, because its inner loop tin be efficiently implemented on most architectures, and in most existent-world data. QuickSort tin be implemented in different ways by changing the option of pivot, so that the worst case rarely occurs for a given blazon of data. Even so, merge sort is mostly considered ameliorate when data is huge and stored in external storage.

Is QuickSort stable ?
The default implementation is not stable. However whatsoever sorting algorithm tin be made stable by because indexes equally comparison parameter.

Is QuickSort In-place ?
Every bit per the wide definition of in-identify algorithm it qualifies every bit an in-identify sorting algorithm as information technology uses extra space only for storing recursive part calls but not for manipulating the input.

What is 3-Way QuickSort?
In simple QuickSort algorithm, nosotros select an element as pivot, partitioning the array effectually pivot and recur for subarrays on left and right of pivot.
Consider an array which has many redundant elements. For example, {1, 4, 2, four, 2, 4, one, two, 4, i, 2, 2, 2, ii, 4, 1, 4, 4, 4}. If 4 is picked as pivot in Simple QuickSort, we set up only one 4 and recursively procedure remaining occurrences. In 3 Way QuickSort, an assortment arr[50..r] is divided in iii parts:
a) arr[l..i] elements less than pivot.
b) arr[i+1..j-1] elements equal to pivot.
c) arr[j..r] elements greater than pivot.
Encounter this for implementation.

How to implement QuickSort for Linked Lists?
QuickSort on Singly Linked List
QuickSort on Doubly Linked List

Can we implement QuickSort Iteratively?
Yes, please refer Iterative Quick Sort.

Why Quick Sort is preferred over MergeSort for sorting Arrays
Quick Sort in its full general class is an in-place sort (i.e. information technology doesn't require whatever extra storage) whereas merge sort requires O(N) extra storage, North cogent the array size which may be quite expensive. Allocating and de-allocating the extra infinite used for merge sort increases the running time of the algorithm. Comparing average complication nosotros find that both blazon of sorts have O(NlogN) average complexity simply the constants differ. For arrays, merge sort loses due to the employ of extra O(N) storage space.
Most practical implementations of Quick Sort use randomized version. The randomized version has expected time complexity of O(nLogn). The worst case is possible in randomized version also, merely worst example doesn't occur for a item blueprint (like sorted array) and randomized Quick Sort works well in practice.
Quick Sort is also a cache friendly sorting algorithm as information technology has skilful locality of reference when used for arrays.
Quick Sort is also tail recursive, therefore tail call optimizations is done.

Why MergeSort is preferred over QuickSort for Linked Lists?
In case of linked lists the example is different mainly due to difference in retention resource allotment of arrays and linked lists. Different arrays, linked list nodes may not exist adjacent in retentivity. Unlike assortment, in linked list, nosotros can insert items in the center in O(1) extra space and O(1) time. Therefore merge operation of merge sort tin can exist implemented without extra space for linked lists.
In arrays, nosotros can practice random access as elements are continuous in memory. Let us say nosotros take an integer (four-byte) array A and let the address of A[0] be 10 then to access A[i], we can direct access the memory at (x + i*iv). Unlike arrays, nosotros can non do random access in linked list. Quick Sort requires a lot of this kind of access. In linked list to admission i'th index, nosotros have to travel each and every node from the head to i'th node every bit we don't have continuous block of memory. Therefore, the overhead increases for quick sort. Merge sort accesses data sequentially and the need of random access is low.

How to optimize QuickSort and then that it takes O(Log n) extra infinite in worst example?
Delight see QuickSort Tail Phone call Optimization (Reducing worst case space to Log north )

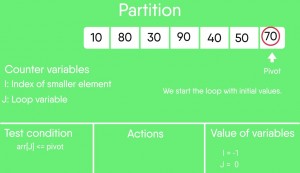
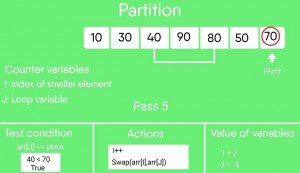
Snapshots:

• Quiz on QuickSort
• Recent Articles on QuickSort
• Coding practice for sorting.

References:
http://en.wikipedia.org/wiki/Quicksort

Other Sorting Algorithms on GeeksforGeeks/GeeksQuiz:
Selection Sort, Bubble Sort, Insertion Sort, Merge Sort, Heap Sort, QuickSort, Radix Sort, Counting Sort, Bucket Sort, ShellSort, Comb Sort, Pigeonhole Sort
Please write comments if you find anything incorrect, or you want to share more information most the topic discussed above.

Source: https://www.geeksforgeeks.org/quick-sort/

Posted by: pahltradjecide.blogspot.com

Share this post